Skip to content

Sabbiu Shah

p-Norms (Taxicab Norm, Euclidean Norm and infinity-norm)

— linear algebra, norms — 1 min read

Norms are a measure of distance. Norm is defined as follows: For p≥1p\geq1,

∣∣x∣∣p≡∣x1∣p+∣x2∣p+...+∣xn∣pp||x||_p \equiv \sqrt[p]{|x_1|^p + |x_2|^p + ... + |x_n|^p}

Taxicab Norm (1-Norm)

When p=1p=1, then the norm is said to be taxicab norm. The distance derived from this norm is called Manhattan distance.

∣∣x∣∣1≡∣x1∣+∣x2∣+...+∣xn∣||x||_1 \equiv |x_1| + |x_2| + ... + |x_n|

Euclidean Norm (2-Norm)

It is the most common notion of distance. When p=2p=2, then the norm is said to be euclidean norm.

∣∣x∣∣2≡∣x1∣2+∣x2∣2+...+∣xn∣2||x||_2 \equiv \sqrt{|x_1|^2 + |x_2|^2 + ... + |x_n|^2}

∞-norm

Infinity norm is defined as,

∣∣x∣∣∞≡max(∣x1∣,∣x2∣,...,∣xn∣)||x||_\infty \equiv max(|x_1|, |x_2|, ..., |x_n|)

Proof

∣∣x∣∣p≡∑i=1n∣xi∣p          Equation of p-norm∣∣x∣∣p≡m∑i=1n∣xi∣pm          m=max(∣xi∣)\begin{aligned} ||x||_p & \equiv \sum_{i=1}^n |x_i|^p\ \ \ \ \ \ \ \ \ \ \text{Equation of p-norm}\\ ||x||_p & \equiv m \sum_{i=1}^n \frac{|x_i|^p}{m}\ \ \ \ \ \ \ \ \ \ m=max(|x_i|)\\ \end{aligned}

As, pp approaches ∞\infty, only the term max∣xi∣m\frac{max|x_i|}{m} equals to 11, while other terms approaches to 00. Thus, ∑i=1n∣xi∣pm=1\sum_{i=1}^n \frac{|x_i|^p}{m} = 1

∴ ∣∣x∣∣∞≡max(∣xi∣)\begin{aligned} \therefore\ ||x||_\infty & \equiv max(|x_i|) \end{aligned}

Visualising norms as a unit circle

This section will show visualization when, ∣∣x∣∣p≡1||x||_p \equiv 1. Let us consider for 2 Dimensional case.

1-Norm

The equation is given as,

∣∣x∣∣1=∣x1∣+∣x2∣  ⟹  1=∣x1∣+∣x2∣\begin{aligned} & ||x||_1 = |x_1| + |x_2|\\ \implies & 1= |x_1| + |x_2|\\ \end{aligned}

Thus we get the following equations,
When x1≥0x_1\geq0 and x2≥0x_2\geq0, x2=1−x1x_2=1-x_1 [First quadrant]
When x1≤0x_1\leq0 and x2≥0x_2\geq0, x2=1+x1x_2=1+x_1 [Second quadrant]
When x1≤0x_1\leq0 and x2≤0x_2\leq0, x2=x1−1x_2=x_1-1 [Third quadrant]
When x1≥0x_1\geq0 and x2≤0x_2\leq0, x2=−x1−1x_2=-x_1-1 [Fourth quadrant]

Plotting these equations, we get,

1-Norm as a unit circle

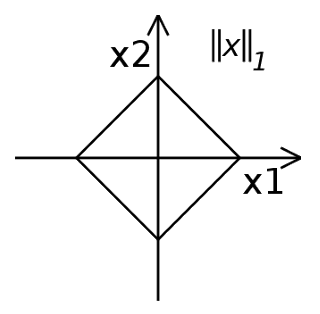
2-Norm

The equation is given as,

∣∣x∣∣2=∣x1∣2+∣x2∣2  ⟹  1=x12+x22\begin{aligned} & ||x||_2 = \sqrt{|x_1|^2 + |x_2|^2}\\ \implies & 1= x_1^2 + x_2^2\\ \end{aligned}

As this equation represents a unit circle, we get the following graph,

2-Norm as a unit circle

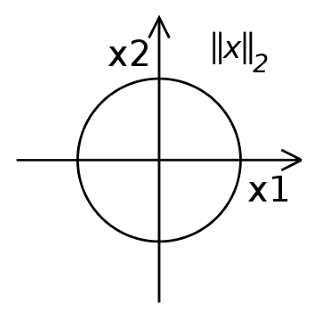
∞-norm

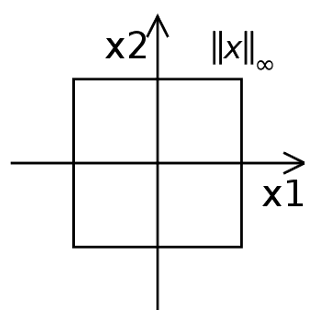
The equation is given as,

∣∣x∣∣∞=max(∣x1∣,∣x2∣)  ⟹  1=max(∣x1∣,∣x2∣)\begin{aligned} & ||x||_\infty = max(|x_1|, |x_2|)\\ \implies & 1 = max(|x_1|, |x_2|)\\ \end{aligned}

This gives the following graph,

infinity-Norm as a unit circle

Substituting different values of p, these equations can be further visualised in Wolfram Mathematica Demonstaration

References

  1. excerpt justin solomon, mathematical methods for robotics, vision, and graphics
  2. wolfram mathematica norms demonstration
  3. wikipedia article on lp space